⇊ Disjoint Compatible Perfect Matchings ⇊

Université Libre de Bruxelles
Computer Science Department
INFO-F420 Computational geometry
(professor Stefan Langerman)
Project

Disjoint Compatible Perfect Matchings

Olivier Pirson OPi — olivier.pirson.opi@gmail.com
April 26, 2017
(Some corrections June 17, 2020)
ULB

Introduction

This Web page presents some properties between two perfect matchings in planar straight line graphs. Below, a simple JavaScript application allows to experiment with these concepts.

1 Some basic definitions

We will consider a particular form of undirected graph, where each vertex is a point in the plane, and each edge is a segment (no curve) between two points. Moreover there is no intersection. We call that a planar straight line graph (PSLG).

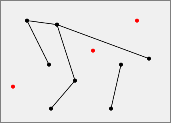
Planar straight line graph
Planar straight line graph example.

A matching (or independent edge set) is a set of segments such that they have no point in common (i.e. if and only if each vertex has degree at most one). In this document we consider only matchings with no intersection.

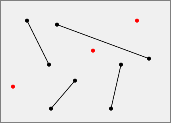
Matching
Matching example.
(If you click on this example or a following example, it will be loaded to the interactive application below.)

A matching is said perfect if and only if each point is an end-point of one and only one segment (i.e. if and only if each vertex has degree one). Of course, that requires an even number of points.

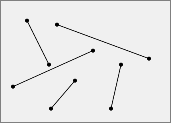
Perfect matching
Perfect matching example.

A matching is said even if and only if it have a even number of segments. Else it said odd.

Now we consider two matchings on a same PSLG. Two matchings are said disjoint if and only if their have no common segment.

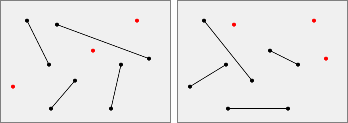
Disjoint matchings
Disjoint matchings example.
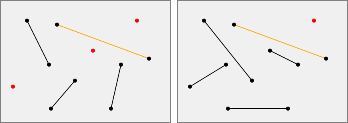
Not disjoint matchings
Not disjoint matchings example.
(Common segments are drawn in orange.)

Two matchings are said compatible if and only if their union is with no intersection.
Be careful, the union is the union of two sets (concept of set theory). And the intersection is the intersection of two segments (geometrical concept).

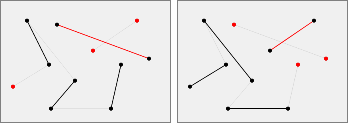
Not compatible matchings
Not compatible matchings example.
(Segments such that the union intersect are drawn in red. And in thin silver are drawn segments of the other matching.)
Not compatible perfect matchings
Not compatible perfect matchings example with one segment in common.

Let $S$ a set of $2n$ points. If we called $p_1, p_2, p_3, \dots, p_{2n}$ in increasing order of their x-coordinates (and for points with the same x-coordinate, in increasing order of their y-coordinates), the canonical perfect matching of $S$, written $N(S)$, is the perfect matching with segments $p_1$—$p_2, p_3$—$p_4, p_5$—$p_6, \dots p_{2n-1}$—$p_{2n}$.

Canonical perfect matching
Canonical perfect matching example.
Perfect matchings
5 out of the 2736 possible perfect matchings for these set of points, where the second is the canonical perfect matching.

2 Transformation between two perfect matchings

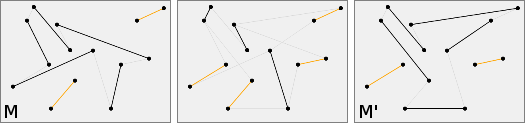
When two perfect matchings are not compatible, it may be possible to have a succession of perfect matchings two by two compatible, from the first one to the last one.

We call transformation between two perfect matchings a sequence of perfect matchings such that each consecutive pair of perfect matchings is compatible. More formally, with $S$ a set of points, $M$ and $M'$ two perfect matchings of $S$, a transformation between $M$ and $M'$ of length $k$ is a sequence $M = M_0, M_1, M_2, \dots, M_k = M'$ of perfect matchings of $S$ such that $\forall i \in \{0, 1, 2, \dots, k-1\}: M_i$ and $M_{i+1}$ are compatible.

Transformation
Transformation example of length 2.

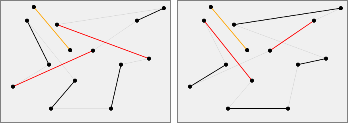
If moreover $\forall i \in \{0, 1, 2, \dots, k-1\}: M_i$ and $M_{i+1}$ are disjoint, the transformation is called a disjoint transformation.

Disjoint transformation
Disjoint transformation example of length 3.

2.1 Lemmas

Lemma ⅰ

$\forall$ perfect matching $M$, $\forall$ line $t$ cutting an even number of segments of $M$ (such that $t$ contains no vertex),
let $H$ the halfplane determined by $t$, let $S$ the set of vertices of $M$ in $H$,
$\exists$ perfect matching $M'$ of $S: M$ and $M'$ are compatible

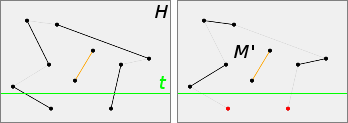
Lemma i
Lemma i example.
The article [1] p. 7 contains two proofs of this lemma, with two different ideas (the concept of segment extensions or thicken segments to infinitesimal triangles).

Lemma ⅱ

$\forall$ perfect matching $M$, $\forall$ line $t$ cutting an even number of segments of $M$ (such that $t$ contains no vertex),
let halfplanes $H_1$ and $H_2$ determined by $t$, let $S_1$ and $S_2$ sets of vertices of $M$ in $H_1$ and in $H_2$,
$\exists$ perfect matchings $M_1$ of $S_1$ and $M_2$ of $S_2: M$ and $(M_1 \cup M_2)$ are compatible

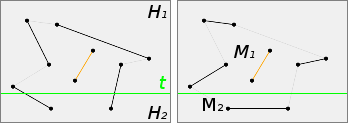
Lemma ii
Lemma ii example.
Proof.

By two applications of lemma ⅰ, there are perfect matchings $M_1$ of $S_1$ and $M_2$ of $S_2$ such that $M$ and $M_1$ are compatible, and $M$ and $M_2$ are compatible. Since $M_1$ and $M_2$ are separated, then $M_1 \cup M_2$ is also a perfect matching and $M$ and $(M_1 \cup M_2)$ are compatible.

Lemma ⅲ

$\forall S$ of $2n$ points, $\forall$ perfect matchings $M$ of $S$, $\exists$ transformation of length at most $\lceil$$\lg(n)$$\rceil$ between $M$ and $N(S)$

Proof by induction on $n$.
  • Base case: $n = 1$. All perfect matchings with 2 points are canonical, so the transformation has length $0 = \lg(1)$.
  • Inductive hypothesis. Assume that the lemma is true for all value less than $n$ with $n > 1$.
  • Inductive step.

    Let a vertical line $t$ cutting the plane in two parts (left $H^l$ and right $H^r$) such that $H^l$ contains a set $S^l$ of $2\lfloor\frac{n}{2}\rfloor$ points and $H^r$ contains a set $S^r$ of $2\lceil\frac{n}{2}\rceil$ points.

    Let $m$ the number of segments cut. The subset of segments in the left that no intersects with $t$ is a perfect matching, so $2\lfloor\frac{n}{2}\rfloor - m$ is even and $m$ too.

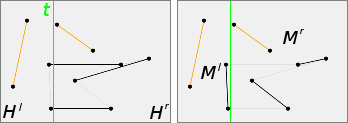
    Lemma iii
    Example with $n = 5: |S^l| = 4$ and $|S^r| = 6$, $m = 2$

    By lemma ⅱ, there is perfect matchings $M^l$ of $S^l$ and $M^r$ of $S^r$ such that $M$ and $(M^l \cup M^r)$ are compatible

    By inductive hypothesis to $M^l$ and $M^r$ there are theses transformations:

    $M^l = M^l_0, M^l_1, M^l_2, \dots, M^l_k = N(S^l)$
    $M^r = M^r_0, M^r_1, M^r_2, \dots, M^r_k = N(S^r)$

    where $\lceil\lg\lfloor\frac{n}{2}\rfloor\rceil \leq \lceil\lg\lceil\frac{n}{2}\rceil\rceil \leq \lceil\lg(n)\rceil - 1 = k$

    $\forall i: M^l_i$ and $M^l_{i+1}$ are compatible, and $M^r_i$ and $M^r_{i+1}$ are compatible.

    Let $M_i = M^l_i \cup M^r_i$. It is a perfect matching of $S$, because $M^l_i$ and $M^r_i$ are separated by $t$. And $M_i$ and $M_{i+1}$ are compatible.

    $N(S) = N(S^l) \cup N(S^r) = M_k$
    so $M, M_0, M_1, M_2, \dots, M_k$ is a transformation between $M$ and $N(S)$ of length $\lg(n)$

2.2 Theorem

Theorem ⅳ

$\forall$ perfect matchings $M$ and $M'$, $\exists$ transformation of length at most $2 \lceil\lg(n)\rceil$ between $M$ and $M'$

Proof.

Let $S$ the set of $2n$ points. By lemma ⅲ there are perfect matchings $M$ and $M'$ such that

$M = M_0, M_1, M_2, \dots, M_k = N(S)$ and
$M' = M'_0, M'_1, M'_2, \dots, M'_{k'} = N(S)$ with $k, k' \leq \lceil\lg(n)\rceil$.

Thus $M_0, M_1, M_2, \dots, M_k = M'_{k'}, \dots, M'_2, M'_1, M'_0 = M'$ is a transformation of length at most $2 \lceil\lg(n)\rceil$.

3 Experiment by yourself

3.1 Interactive application

Click in the two zones to add/remove point or segment (only one segment by point and with no intersection). You can also click on one matching example to load it in the interactive zones. Wait a moment above a button to bring up a short explanation tooltip.

…
  • :
  • :
  • :

3.2 Some explanations

You can add or remove points one by one, but only perfect matchings are useful. Isolated points are drawing in red. To remove a point, click on it. When a point is removed, all its segment are removed.

To add a segment, click to add the first point, then click to add the second point and the segment. It is impossible to add a segment to a point that already belongs to a segment, or to add a segment that intersects with an other segment. To remove a segment (and keeping its points), click to a first point and then to the second point.

If a matching is a canonical perfect matching then it is in a blue frame.

For two consecutive matchings in the list, common segments are in orange and segments that intersects between them are in red.

By default, all segments of the immediately previous and next matchings are drawn in thin silver. An option permits to draw all segments that are in at least one matching in the list, or on the contrary to disable that and to draw only the segments of the matching.

For the matchings of the two interactive zones, some properties are displayed. Below that, some global properties between these two matchings are also displayed.

The matching of the left interactive zone is also displayed in the first position in the list. And the matching of the right interactive zone is displayed in the last position. Between them, are displayed all other perfect matchings or the intermediary perfect matchings to be a transformation.

Build all perfect matchings or build a shortest transformation are very expensive operations, so they are impossible with a lot of points. Moreover only transformations of length 2 and 3 are tried.

The upper bound given by the application for the number of possible perfect matchings is very rough. In fact it is the number of general (with possible intersection) perfect matchings.

With $n = 2k$: $|\{\text{general perfect matching}\}| = (n - 1).(n - 3).(n - 5) … 5 . 3 = \frac{n!}{n.(n - 2).(n - 4) … 4 . 2} = \frac{n!}{2^k . k!}$.

And the Stirling’s approximation $n! \sim \sqrt{2 \pi n} (\frac{n}{e})^n$ give the approximation $\sqrt{2} (\frac{n}{e})^k$.

3.3 Sources code

The interactive application was tested on Firefox 52.0 (and a little on Chromium 57.0) (requires ECMAScript/JavaScript 2015 6th and modern browser).

4 Compatible matching conjecture

Compatible matching conjecture

$\forall$ even perfect matching $M$, $\exists$ perfect matching $M': M$ and $M'$ are disjoint and compatible

First observation: the even condition is necessary. Indeed, it is easy to find simple odd perfect matching $M$ such that doesn't exist a disjoint and compatible perfect matching $M'$. In the example below, for the first perfect matching with $3$ segments we see that none of four other perfect matchings is appropriate. (In fact for this example, there is only one possible pair $(M, M')$, the 2nd and the 5th matchings.)

Odd perfect matching
Odd perfect matching example, with no disjoint and compatible other matching.

The article [1] p. 9 explains how construct odd perfect matching with arbitrary size with no disjoint and compatible other matching. The idea is to consider the canonical perfect matching on points disposed on a circle like this:

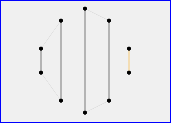
Odd perfect matching
Odd perfect matching example disposed on a circle, with no disjoint and compatible other matching.

This conjecture was proved in the article [3].

References

Index

↑

Contents

↓
+ ☰